At What Time Is the Velocity Again Zero? Express Your Answer With the Appropriate Units

iii Motility Along a Straight Line

3.vi Finding Velocity and Displacement from Acceleration

Learning Objectives

By the terminate of this section, you will be able to:

Derive the kinematic equations for constant dispatch using integral calculus.
Use the integral formulation of the kinematic equations in analyzing movement.
Find the functional form of velocity versus time given the acceleration function.
Find the functional class of position versus time given the velocity function.

This section assumes y'all have enough background in calculus to be familiar with integration. In Instantaneous Velocity and Speed and Average and Instantaneous Acceleration we introduced the kinematic functions of velocity and acceleration using the derivative. By taking the derivative of the position role we found the velocity role, and likewise past taking the derivative of the velocity function we found the acceleration office. Using integral calculus, we tin can work backward and summate the velocity function from the acceleration role, and the position function from the velocity function.

Kinematic Equations from Integral Calculus

Let's begin with a particle with an acceleration a(t) is a known office of fourth dimension. Since the fourth dimension derivative of the velocity function is acceleration,

$\frac{d}{dt}v(t)=a(t),$

we can accept the indefinite integral of both sides, finding

$\int \frac{d}{dt}v(t)dt=\int a(t)dt+{C}_{1},$

where C ₁ is a constant of integration. Since

$\int \frac{d}{dt}v(t)dt=v(t)$

, the velocity is given past

$v(t)=\int a(t)dt+{C}_{1}.$

Similarly, the time derivative of the position office is the velocity function,

$\frac{d}{dt}x(t)=v(t).$

Thus, we can use the same mathematical manipulations we just used and discover

$x(t)=\int v(t)dt+{C}_{2},$

where C ₂ is a second constant of integration.

Nosotros can derive the kinematic equations for a constant acceleration using these integrals. With a(t) = a a constant, and doing the integration in (Figure), we observe

$v(t)=\int adt+{C}_{1}=at+{C}_{1}.$

If the initial velocity is v(0) = v ₀, and then

${v}_{0}=0+{C}_{1}.$

And then, C _one = v ₀ and

$v(t)={v}_{0}+at,$

which is (Equation). Substituting this expression into (Figure) gives

$x(t)=\int ({v}_{0}+at)dt+{C}_{2}.$

Doing the integration, we discover

$x(t)={v}_{0}t+\frac{1}{2}a{t}^{2}+{C}_{2}.$

If x(0) = 10 ₀, we have

${x}_{0}=0+0+{C}_{2};$

so, C ₂ = x ₀. Substituting back into the equation for x(t), we finally have

$x(t)={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2},$

which is (Equation).

Case

Motion of a Motorboat

A motorboat is traveling at a constant velocity of v.0 grand/s when it starts to decelerate to arrive at the dock. Its acceleration is

$a(t)=-\frac{1}{4}t\,\text{m/}{\text{s}}^{2}$

. (a) What is the velocity function of the motorboat? (b) At what fourth dimension does the velocity reach zero? (c) What is the position part of the motorboat? (d) What is the deportation of the motorboat from the time it begins to decelerate to when the velocity is nix? (e) Graph the velocity and position functions.

Strategy

(a) To get the velocity part nosotros must integrate and utilise initial conditions to find the constant of integration. (b) We set the velocity office equal to aught and solve for t. (c) Similarly, we must integrate to find the position part and use initial conditions to find the abiding of integration. (d) Since the initial position is taken to be nix, we simply accept to evaluate the position function at

$t=0$

Solution

Nosotros take t = 0 to be the fourth dimension when the boat starts to decelerate.

From the functional grade of the dispatch we can solve (Figure) to get 5(t):

[reveal-reply q="136447″]Evidence Answer[/reveal-answer]
[hidden-reply a="136447″]

$v(t)=\int a(t)dt+{C}_{1}=\int -\frac{1}{4}tdt+{C}_{1}=-\frac{1}{8}{t}^{2}+{C}_{1}.$

At t = 0 we have v(0) = 5.0 m/south = 0 + C1, so C1 = five.0 1000/s or

$v(t)=5.0\,\text{m/}\text{s}-\frac{1}{8}{t}^{2}$

.[/hidden-answer]
[reveal-reply q="967265″]Show Answer[/reveal-respond]
[subconscious-answer a="967265″]
$v(t)=0=5.0\,\text{m/}\text{s}-\frac{1}{8}{t}^{2}⇒t=6.3\,\text{s}$

[/hidden-answer]
Solve (Figure):

[reveal-answer q="251505″]Bear witness Answer[/reveal-respond]
[hidden-answer a="251505″]

$x(t)=\int v(t)dt+{C}_{2}=\int (5.0-\frac{1}{8}{t}^{2})dt+{C}_{2}=5.0t-\frac{1}{24}{t}^{3}+{C}_{2}.$

At t = 0, nosotros set ten(0) = 0 = x0, since we are only interested in the deportation from when the gunkhole starts to decelerate. Nosotros have

$x(0)=0={C}_{2}.$

Therefore, the equation for the position is

$x(t)=5.0t-\frac{1}{24}{t}^{3}.$

[/hidden-answer]
[reveal-answer q="330950″]Bear witness Answer[/reveal-answer]
[hidden-answer a="330950″]Since the initial position is taken to exist cipher, we merely take to evaluate x(t) when the velocity is zero. This occurs at t = 6.iii s. Therefore, the displacement is
$x(6.3)=5.0(6.3)-\frac{1}{24}{(6.3)}^{3}=21.1\,\text{m}\text{.}$

[/hidden-answer]

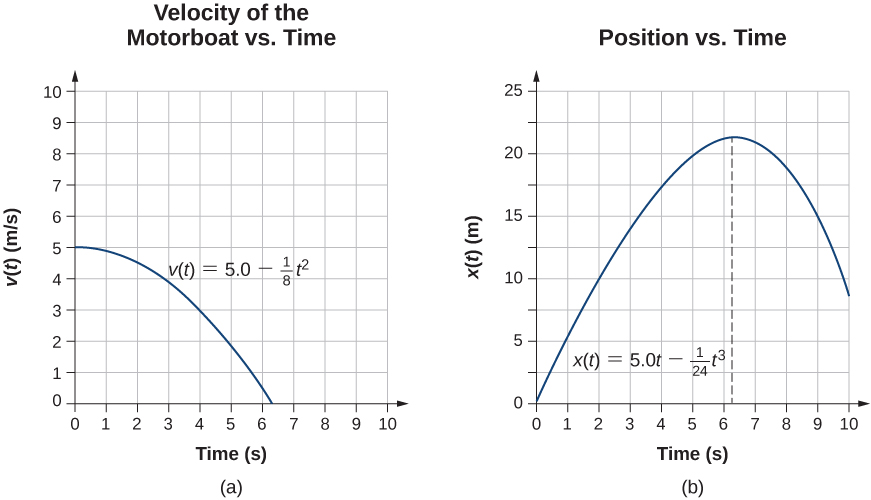
Graph A is a plot of velocity in meters per second as a function of time in seconds. Velocity is five meters per second at the beginning and decreases to zero. Graph B is a plot of position in meters as a function of time in seconds. Position is zero at the beginning, increases reaching maximum between six and seven seconds, and then starts to decrease. — **Figure 3.30** (a) Velocity of the motorboat as a function of time. The motorboat decreases its velocity to nil in vi.3 southward. At times greater than this, velocity becomes negative—meaning, the boat is reversing management. (b) Position of the motorboat as a function of time. At t = 6.3 s, the velocity is zippo and the boat has stopped. At times greater than this, the velocity becomes negative—meaning, if the boat continues to motility with the same acceleration, it reverses direction and heads dorsum toward where it originated.

Significance

The dispatch part is linear in time so the integration involves simple polynomials. In (Effigy), we encounter that if nosotros extend the solution beyond the point when the velocity is nil, the velocity becomes negative and the gunkhole reverses direction. This tells the states that solutions can give us data exterior our immediate interest and we should be careful when interpreting them.

Cheque Your Agreement

A particle starts from remainder and has an acceleration role

$5-10t{\text{m/s}}^{2}$

. (a) What is the velocity office? (b) What is the position function? (c) When is the velocity zero?

[reveal-answer q="fs-id1168057352922″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168057352922″]

The velocity function is the integral of the acceleration function plus a constant of integration. By (Effigy),
$v(t)=\int a(t)dt+{C}_{1}=\int (5-10t)dt+{C}_{1}=5t-5{t}^{2}+{C}_{1}.$

Since v(0) = 0, we take C ₁ = 0; and then,

$v(t)=5t-5{t}^{2}.$
By (Effigy),
$x(t)=\int v(t)dt+{C}_{2}=\int (5t-5{t}^{2})dt+{C}_{2}=\frac{5}{2}{t}^{2}-\frac{5}{3}{t}^{3}+{C}_{2}$

.Since 10(0) = 0, nosotros have C _two = 0, and

$x(t)=\frac{5}{2}{t}^{2}-\frac{5}{3}{t}^{3}.$
The velocity can exist written as v(t) = vt(1 – t), which equals nothing at t = 0, and t = 1 s.

[/subconscious-respond]

Summary

Integral calculus gives us a more complete conception of kinematics.
If acceleration a(t) is known, we tin use integral calculus to derive expressions for velocity five(t) and position x(t).
If acceleration is abiding, the integral equations reduce to (Effigy) and (Effigy) for motility with abiding acceleration.

Key Equations

Displacement	$\text{Δ}x={x}_{\text{f}}-{x}_{\text{i}}$
Total displacement	$\text{Δ}{x}_{\text{Total}}=\sum \text{Δ}{x}_{\text{i}}$
Average velocity	$\overset{\text{-}}{v}=\frac{\text{Δ}x}{\text{Δ}t}=\frac{{x}_{2}-{x}_{1}}{{t}_{2}-{t}_{1}}$
Instantaneous velocity	$v(t)=\frac{dx(t)}{dt}$
Average speed	$\text{Average speed}=\overset{\text{-}}{s}=\frac{\text{Total distance}}{\text{Elapsed time}}$
Instantaneous speed	$\text{Instantaneous speed}=\|v(t)\|$
Average acceleration	$\overset{\text{-}}{a}=\frac{\text{Δ}v}{\text{Δ}t}=\frac{{v}_{f}-{v}_{0}}{{t}_{f}-{t}_{0}}$
Instantaneous acceleration	$a(t)=\frac{dv(t)}{dt}$
Position from average velocity	$x={x}_{0}+\overset{\text{-}}{v}t$
Average velocity	$\overset{\text{-}}{v}=\frac{{v}_{0}+v}{2}$
Velocity from dispatch	$v={v}_{0}+at\enspace(\text{constant}\,a\text{)}$
Position from velocity and acceleration	$x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}\enspace(\text{constant}\,a\text{)}$
Velocity from altitude	${v}^{2}={v}_{0}^{2}+2a(x-{x}_{0})\enspace(\text{constant}\,a\text{)}$
Velocity of gratuitous fall	$v={v}_{0}-gt\,\text{(positive upward)}$
Height of free fall	$y={y}_{0}+{v}_{0}t-\frac{1}{2}g{t}^{2}$
Velocity of costless fall from height	${v}^{2}={v}_{0}^{2}-2g(y-{y}_{0})$
Velocity from acceleration	$v(t)=\int a(t)dt+{C}_{1}$
Position from velocity	$x(t)=\int v(t)dt+{C}_{2}$

Conceptual Questions

When given the acceleration function, what additional information is needed to find the velocity part and position office?

Problems

The acceleration of a particle varies with time according to the equation

$a(t)=p{t}^{2}-q{t}^{3}$

. Initially, the velocity and position are zero. (a) What is the velocity as a function of time? (b) What is the position as a part of time?

Between t = 0 and t = t ₀, a rocket moves straight upward with an acceleration given past

$a(t)=A-B{t}^{1\,\text{/}2}$

, where A and B are constants. (a) If x is in meters and t is in seconds, what are the units of A and B? (b) If the rocket starts from rest, how does the velocity vary between t = 0 and t = t ₀? (c) If its initial position is zero, what is the rocket'south position equally a function of time during this aforementioned time interval?

[reveal-answer q="fs-id1168055134758″]Show Solution[/reveal-reply]

[hidden-reply a="fs-id1168055134758″]

$A={\text{m/s}}^{2}\enspaceB={\text{m/s}}^{5\,\text{/}2}$

;
b.

$\begin{array}{cc} v(t)=\int a(t)dt+{C}_{1}=\int (A-B{t}^{1\,\text{/}2})dt+{C}_{1}=At-\frac{2}{3}B{t}^{3\,\text{/}2}+{C}_{1}\hfill \\ v(0)=0={C}_{1}\enspace\text{so}\enspacev({t}_{0})=A{t}_{0}-\frac{2}{3}B{t}_{0}^{\text{3/2}}\hfill \end{array}$

;

$\begin{array}{cc} x(t)=\int v(t)dt+{C}_{2}=\int (At-\frac{2}{3}B{t}^{3\,\text{/}2})dt+{C}_{2}=\frac{1}{2}A{t}^{2}-\frac{4}{15}B{t}^{5\,\text{/}2}+{C}_{2}\hfill \\ x(0)=0={C}_{2}\enspace\text{so}\enspacex({t}_{0})=\frac{1}{2}A{t}_{0}^{2}-\frac{4}{15}B{t}_{0}^{\text{5/2}}\hfill \end{array}$

[/hidden-answer]

The velocity of a particle moving forth the ten-axis varies with time according to

$v(t)=A+B{t}^{-1}$

, where A = 2 m/s, B = 0.25 1000, and

$1.0\,\text{s}\le t\le 8.0\,\text{s}$

. Make up one's mind the dispatch and position of the particle at t = ii.0 s and t = 5.0 s. Assume that

$x(t=1\,\text{s})=0$

A particle at rest leaves the origin with its velocity increasing with time according to v(t) = 3.2t m/s. At 5.0 s, the particle's velocity starts decreasing according to [16.0 – 1.5(t – 5.0)] thousand/due south. This decrease continues until t = 11.0 s, after which the particle's velocity remains constant at 7.0 m/due south. (a) What is the acceleration of the particle as a function of fourth dimension? (b) What is the position of the particle at t = two.0 s, t = 7.0 southward, and t = 12.0 s?

[reveal-reply q="fs-id1168055121296″]Bear witness Solution[/reveal-answer]

[subconscious-answer a="fs-id1168055121296″]

$\begin{array}{cc} a(t)=3.2{\text{m/s}}^{2}\enspacet\le 5.0\,\text{s}\hfill \\ a(t)=1.5{\text{m/s}}^{2}\enspace5.0\,\text{s}\le t\le 11.0\,\text{s}\hfill \\ a(t)=0{\text{m/s}}^{2}\enspacet>11.0\,\text{s}\hfill \end{array}$

;
b.

$\begin{array}{cc} x(t)=\int v(t)dt+{C}_{2}=\int 3.2tdt+{C}_{2}=1.6{t}^{2}+{C}_{2}\hfill \\ \quad t\le 5.0\,\text{s}\hfill \\ x(0)=0⇒{C}_{2}=0\enspace\text{therefore,}\,x(2.0\,\text{s})=6.4\,\text{m}\hfill \\ x(t)=\int v(t)dt+{C}_{2}=\int [16.0-1.5(t-5.0)]dt+{C}_{2}=16t-1.5(\frac{{t}^{2}}{2}-5.0t)+{C}_{2}\hfill \\ 5.0\le t\le 11.0\,\text{s}\hfill \\ x(5\,\text{s})=1.6{(5.0)}^{2}=40\,\text{m}=16(5.0\,\text{s})-1.5(\frac{{5}^{2}}{2}-5.0(5.0))+{C}_{2}\hfill \\ \quad 40=98.75+{C}_{2}⇒{C}_{2}=-58.75\hfill \\ x(7.0\,\text{s})=16(7.0)-1.5(\frac{{7}^{2}}{2}-5.0(7))-58.75=69\,\text{m}\hfill \\ \quad x(t)=\int 7.0dt+{C}_{2}=7t+{C}_{2}\hfill \\ \phantom{\rule{1.5em}{0ex}}t\ge 11.0\,\text{s}\hfill \\ x(11.0\,\text{s})=16(11)-1.5(\frac{{11}^{2}}{2}-5.0(11))-58.75=109=7(11.0\,\text{s})+{C}_{2}⇒{C}_{2}=32\,\text{m}\hfill \\ \quad x(t)=7t+32\,\text{m}\hfill \\ \phantom{\rule{1.5em}{0ex}}x\ge 11.0\,\text{s}⇒x(12.0\,\text{s})=7(12)+32=116\,\text{m}\hfill \end{array}$

[/subconscious-respond]

Additional Problems

Professional baseball player Nolan Ryan could pitch a baseball game at approximately 160.0 km/h. At that boilerplate velocity, how long did it have a ball thrown by Ryan to achieve home plate, which is 18.iv m from the pitcher's mound? Compare this with the average reaction time of a homo to a visual stimulus, which is 0.25 s.

An aeroplane leaves Chicago and makes the 3000-km trip to Los Angeles in v.0 h. A 2nd plane leaves Chicago half hour later and arrives in Los Angeles at the same fourth dimension. Compare the boilerplate velocities of the two planes. Ignore the curvature of Globe and the difference in altitude between the two cities.

[reveal-reply q="fs-id1168055151090″]Show Solution[/reveal-answer]

[hidden-reply a="fs-id1168055151090″]

Take west to be the positive direction.

1st aeroplane:

$\overset{\text{-}}{\nu }=600\,\text{km/h}$

second plane

$\overset{\text{-}}{\nu }=667.0\,\text{km/h}$

[/subconscious-reply]

Unreasonable Results A cyclist rides xvi.0 km east, then viii.0 km west, then 8.0 km eastward, then 32.0 km west, and finally 11.2 km due east. If his average velocity is 24 km/h, how long did it accept him to complete the trip? Is this a reasonable fourth dimension?

An object has an dispatch of

$+1.2\,{\text{cm/s}}^{2}$

. At

$t=4.0\,\text{s}$

, its velocity is

$-3.4\,\text{cm/s}$

. Determine the object's velocities at

$t=1.0\,\text{s}$

and

$t=6.0\,\text{s}$

[reveal-answer q="fs-id1168055302745″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168055302745″]

$a=\frac{v-{v}_{0}}{t-{t}_{0}}$

$t=0,\,a=\frac{-3.4\,\text{cm/s}-{v}_{0}}{4\,\text{s}}=1.2\,{\text{cm/s}}^{2}⇒{v}_{0}=-8.2\,\text{cm/s}$

$v={v}_{0}+at=-8.2+1.2\,t$

;

$v=-7.0\,\text{cm/s}\enspacev=-1.0\,\text{cm/s}$

[/subconscious-answer]

A particle moves forth the 10-centrality according to the equation

$x(t)=2.0-4.0{t}^{2}$

yard. What are the velocity and dispatch at

$t=2.0$

s and

$t=5.0$

A particle moving at constant dispatch has velocities of

$2.0\,\text{m/s}$

$t=2.0$

south and

$-7.6\,\text{m/s}$

$t=5.2$

southward. What is the acceleration of the particle?

[reveal-answer q="fs-id1168055307822″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1168055307822″]

$a=-3\,{\text{m/s}}^{2}$

[/hidden-respond]

A train is moving up a steep grade at constant velocity (run into post-obit figure) when its caboose breaks loose and starts rolling freely along the track. After 5.0 s, the caboose is 30 grand behind the railroad train. What is the dispatch of the caboose?

Figure shows a train moving up a hill.

An electron is moving in a straight line with a velocity of

$4.0\,×\,{10}^{5}$

1000/southward. Information technology enters a region 5.0 cm long where it undergoes an acceleration of

$6.0\,×\,{10}^{12}\,{\text{m/s}}^{2}$

along the same straight line. (a) What is the electron's velocity when information technology emerges from this region? b) How long does the electron take to cross the region?

[reveal-answer q="fs-id1168055302554″]Testify Solution[/reveal-respond]

[hidden-answer a="fs-id1168055302554″]

$v=8.7\,×\,{10}^{5}\,\text{m/s}$

;

$t=7.8\,×\,{10}^{-8}\,\text{s}$

[/hidden-respond]

An ambulance driver is rushing a patient to the hospital. While traveling at 72 km/h, she notices the traffic light at the upcoming intersections has turned amber. To accomplish the intersection before the lite turns red, she must travel 50 one thousand in 2.0 s. (a) What minimum dispatch must the ambulance take to reach the intersection earlier the lite turns cherry-red? (b) What is the speed of the ambulance when it reaches the intersection?

A motorcycle that is slowing downwardly uniformly covers 2.0 successive km in 80 s and 120 s, respectively. Summate (a) the acceleration of the motorcycle and (b) its velocity at the commencement and end of the ii-km trip.

[reveal-answer q="fs-id1168057524743″]Evidence Solution[/reveal-answer]

[hidden-answer a="fs-id1168057524743″]

$1\,\text{km}={v}_{0}(80.0\,\text{s})+\frac{1}{2}a{(80.0)}^{2}$

;

$2\,\text{km}={v}_{0}(200.0)+\frac{1}{2}a{(200.0)}^{2}$

solve simultaneously to get

$a=-\frac{0.1}{2400.0}{\text{km/s}}^{2}$

and

${v}_{0}=0.014167\,\text{km/s}$

, which is

$51.0\,\text{km/h}$

. Velocity at the stop of the trip is

$v=21.0\,\text{km/h}$

.
[/subconscious-respond]

A cyclist travels from point A to point B in 10 min. During the beginning ii.0 min of her trip, she maintains a uniform acceleration of

$0.090\,{\text{m/s}}^{2}$

. She then travels at constant velocity for the next 5.0 min. Next, she decelerates at a constant rate so that she comes to a rest at point B iii.0 min subsequently. (a) Sketch the velocity-versus-fourth dimension graph for the trip. (b) What is the acceleration during the last 3 min? (c) How far does the cyclist travel?

Two trains are moving at 30 m/s in opposite directions on the same rail. The engineers run into simultaneously that they are on a collision course and employ the brakes when they are 1000 one thousand apart. Assuming both trains have the aforementioned dispatch, what must this acceleration be if the trains are to cease just short of colliding?

[reveal-answer q="fs-id1168055171872″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168055171872″]

$a=-0.9\,{\text{m/s}}^{2}$

[/subconscious-reply]

A 10.0-m-long truck moving with a constant velocity of 97.0 km/h passes a 3.0-m-long car moving with a constant velocity of 80.0 km/h. How much time elapses between the moment the front of the truck is even with the back of the car and the moment the dorsum of the truck is even with the front of the car?

A police automobile waits in hiding slightly off the highway. A speeding car is spotted by the police force car doing xl m/southward. At the instant the speeding car passes the police car, the law automobile accelerates from rest at 4 m/s² to grab the speeding automobile. How long does information technology accept the police automobile to catch the speeding automobile?

[reveal-answer q="fs-id1168055306834″]Testify Solution[/reveal-respond]

[hidden-reply a="fs-id1168055306834″]

Equation for the speeding motorcar: This car has a constant velocity, which is the boilerplate velocity, and is not accelerating, so use the equation for deportation with

${x}_{0}=0$

$x={x}_{0}+\overset{\text{-}}{v}t=\overset{\text{-}}{v}t$

; Equation for the police car: This car is accelerating, so use the equation for displacement with

${x}_{0}=0$

and

${v}_{0}=0$

, since the constabulary car starts from balance:

$x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{2}=\frac{1}{2}a{t}^{2}$

; Now nosotros have an equation of motion for each car with a common parameter, which can exist eliminated to find the solution. In this case, nosotros solve for

$t$

. Pace 1, eliminating

$x$

$x=\overset{\text{-}}{v}t=\frac{1}{2}a{t}^{2}$

; Step 2, solving for

$t$

$t=\frac{2\overset{\text{-}}{v}}{a}$

. The speeding machine has a constant velocity of forty g/s, which is its boilerplate velocity. The dispatch of the police motorcar is 4 m/southward². Evaluating t, the fourth dimension for the constabulary car to achieve the speeding machine, we have

$t=\frac{2\overset{\text{-}}{v}}{a}=\frac{2(40)}{4}=20\,\text{s}$

.
[/hidden-answer]

Pablo is running in a half marathon at a velocity of 3 m/due south. Some other runner, Jacob, is fifty meters backside Pablo with the same velocity. Jacob begins to accelerate at 0.05 thousand/due south². (a) How long does it have Jacob to catch Pablo? (b) What is the distance covered by Jacob? (c) What is the final velocity of Jacob?

Unreasonable results A runner approaches the stop line and is 75 1000 abroad; her average speed at this position is eight m/s. She decelerates at this point at 0.5 m/s². How long does information technology take her to cross the finish line from 75 m away? Is this reasonable?

[reveal-answer q="fs-id1168055381859″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168055381859″]

At this acceleration she comes to a full cease in

$t=\frac{-{v}_{0}}{a}=\frac{8}{0.5}=16\,\text{s}$

, merely the altitude covered is

$x=8\,\text{m/s(16}\,\text{s)}-\frac{1}{2}(0.5){(16\,\text{s})}^{2}=64\,\text{m}$

, which is less than the distance she is away from the finish line, so she never finishes the race.
[/hidden-answer]

An airplane accelerates at v.0 m/s^two for 30.0 s. During this time, it covers a distance of 10.0 km. What are the initial and final velocities of the airplane?

Compare the distance traveled of an object that undergoes a change in velocity that is twice its initial velocity with an object that changes its velocity by four times its initial velocity over the same time period. The accelerations of both objects are constant.

[reveal-reply q="fs-id1168055323241″]Evidence Solution[/reveal-reply]

[hidden-reply a="fs-id1168055323241″]

${x}_{1}=\frac{3}{2}{v}_{0}t$

${x}_{2}=\frac{5}{3}{x}_{1}$

[/hidden-respond]

An object is moving east with a constant velocity and is at position

${x}_{0}\,\text{at}\,\text{time}\,{t}_{0}=0$

. (a) With what acceleration must the object take for its full displacement to be zip at a afterward time t ? (b) What is the physical estimation of the solution in the case for

$t\to \infty$

A ball is thrown straight upwardly. It passes a 2.00-thou-high window 7.50 m off the ground on its path up and takes ane.xxx s to go past the window. What was the ball's initial velocity?

[reveal-reply q="fs-id1168055391633″]Show Solution[/reveal-respond]

[hidden-answer a="fs-id1168055391633″]

${v}_{0}=7.9\,\text{m/s}$

velocity at the lesser of the window.

$v=7.9\,\text{m/s}$

${v}_{0}=14.1\,\text{m/s}$

[/hidden-reply]

A coin is dropped from a gasbag balloon that is 300 m to a higher place the basis and rising at 10.0 m/s upward. For the coin, find (a) the maximum height reached, (b) its position and velocity 4.00 south after existence released, and (c) the fourth dimension earlier it hits the basis.

A soft tennis brawl is dropped onto a hard floor from a meridian of 1.l 1000 and rebounds to a acme of one.10 one thousand. (a) Calculate its velocity just before it strikes the floor. (b) Calculate its velocity just after it leaves the flooring on its way back upwardly. (c) Calculate its dispatch during contact with the floor if that contact lasts 3.50 ms

$(3.50\,×\,{10}^{-3}\,\text{s})$

(d) How much did the brawl compress during its standoff with the floor, bold the floor is absolutely rigid?

[reveal-answer q="fs-id1168055325521″]Evidence Solution[/reveal-respond]

[hidden-answer a="fs-id1168055325521″]

$v=5.42\,\text{m/s}$

;
b.

$v=4.64\,\text{m/s}$

;

$a=2874.28\,{\text{m/s}}^{2}$

;

$(x-{x}_{0})=5.11\,×\,{10}^{-3}\,\text{m}$

[/hidden-answer]

Unreasonable results. A raindrop falls from a deject 100 m above the ground. Neglect air resistance. What is the speed of the raindrop when it hits the ground? Is this a reasonable number?

Compare the time in the air of a basketball player who jumps one.0 m vertically off the flooring with that of a player who jumps 0.iii chiliad vertically.

[reveal-respond q="fs-id1168057418927″]Bear witness Solution[/reveal-answer]

[hidden-answer a="fs-id1168057418927″]

Consider the players fall from residuum at the height ane.0 g and 0.3 m.

0.9 southward

0.5 s

[/subconscious-answer]

Suppose that a person takes 0.5 due south to react and motion his paw to catch an object he has dropped. (a) How far does the object fall on Earth, where

$g=9.8\,{\text{m/s}}^{2}?$

(b) How far does the object fall on the Moon, where the dispatch due to gravity is 1/6 of that on Earth?

A hot-air balloon rises from ground level at a constant velocity of three.0 m/s. One infinitesimal after liftoff, a sandbag is dropped accidentally from the balloon. Calculate (a) the time information technology takes for the sandbag to achieve the ground and (b) the velocity of the sandbag when it hits the ground.

[reveal-respond q="fs-id1168055469821″]Show Solution[/reveal-respond]

[subconscious-answer a="fs-id1168055469821″]

$t=6.37\,\text{s}$

taking the positive root;
b.

$v=59.5\,\text{m/s}$

[/hidden-answer]

(a) A world record was prepare for the men'southward 100-thou dash in the 2008 Olympic Games in Beijing by Usain Commodities of Jamaica. Bolt "coasted" across the finish line with a fourth dimension of ix.69 s. If we assume that Bolt accelerated for iii.00 s to reach his maximum speed, and maintained that speed for the balance of the race, calculate his maximum speed and his acceleration. (b) During the same Olympics, Commodities also set the world record in the 200-m dash with a fourth dimension of nineteen.xxx s. Using the same assumptions as for the 100-m dash, what was his maximum speed for this race?

An object is dropped from a acme of 75.0 1000 to a higher place ground level. (a) Determine the distance traveled during the beginning second. (b) Make up one's mind the last velocity at which the object hits the ground. (c) Decide the altitude traveled during the terminal second of motion before hitting the ground.

[reveal-respond q="fs-id1168055273683″]Show Solution[/reveal-reply]

[hidden-answer a="fs-id1168055273683″]

$y=4.9\,\text{m}$

;
b.

$v=38.3\,\text{m/s}$

;

$-33.3\,\text{m}$

[/hidden-answer]

A steel ball is dropped onto a hard flooring from a height of 1.l m and rebounds to a peak of 1.45 m. (a) Calculate its velocity only earlier information technology strikes the floor. (b) Summate its velocity just after it leaves the flooring on its mode back up. (c) Calculate its acceleration during contact with the flooring if that contact lasts 0.0800 ms

$(8.00\,×\,{10}^{-5}\,\text{s})$

(d) How much did the ball compress during its standoff with the flooring, assuming the floor is admittedly rigid?

An object is dropped from a roof of a building of meridian h. During the last second of its descent, information technology drops a distance h/iii. Calculate the height of the building.

[reveal-respond q="fs-id1168055491899″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168055491899″]

$h=\frac{1}{2}g{t}^{2}$

, h = full tiptop and fourth dimension to drop to basis

$\frac{2}{3}h=\frac{1}{2}g{(t-1)}^{2}$

in t – one seconds it drops two/3h

$\frac{2}{3}(\frac{1}{2}g{t}^{2})=\frac{1}{2}g{(t-1)}^{2}$

$\frac{{t}^{2}}{3}=\frac{1}{2}{(t-1)}^{2}$

$0={t}^{2}-6t+3$

$t=\frac{6±\sqrt{{6}^{2}-4·3}}{2}=3±\frac{\sqrt{24}}{2}$

t = 5.45 s and h = 145.5 thou. Other root is less than i due south. Check for t = 4.45 s

$h=\frac{1}{2}g{t}^{2}=97.0$

1000

$=\frac{2}{3}(145.5)$

[/hidden-answer]

Claiming Problems

In a 100-m race, the winner is timed at 11.2 s. The second-place finisher's time is 11.6 s. How far is the second-identify finisher behind the winner when she crosses the finish line? Assume the velocity of each runner is constant throughout the race.

The position of a particle moving forth the 10-axis varies with time according to

$x(t)=5.0{t}^{2}-4.0{t}^{3}$

m. Find (a) the velocity and acceleration of the particle every bit functions of time, (b) the velocity and acceleration at t = two.0 s, (c) the time at which the position is a maximum, (d) the time at which the velocity is nil, and (east) the maximum position.

[reveal-answer q="fs-id1168055269782″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1168055269782″]

$v(t)=10t-12{t}^{2}\text{m/s,}\,a(t)=10-24t\,{\text{m/s}}^{2}$

;
b.

$v(2\,\text{s})=-28\,\text{m/s,}\,a(2\,\text{s})=-38{\text{m/s}}^{2}$

; c. The slope of the position function is zilch or the velocity is zero. There are two possible solutions: t = 0, which gives x = 0, or t = 10.0/12.0 = 0.83 southward, which gives x = 1.16 grand. The second answer is the correct option; d. 0.83 s (eastward) 1.sixteen m

[/hidden-answer]

A cyclist sprints at the cease of a race to assure a victory. She has an initial velocity of 11.5 m/s and accelerates at a charge per unit of 0.500 k/south² for seven.00 due south. (a) What is her final velocity? (b) The cyclist continues at this velocity to the finish line. If she is 300 m from the finish line when she starts to accelerate, how much time did she relieve? (c) The 2d-identify winner was 5.00 yard alee when the winner started to advance, just he was unable to accelerate, and traveled at eleven.8 m/south until the finish line. What was the difference in finish time in seconds between the winner and runner-upwardly? How far back was the runner-up when the winner crossed the cease line?

In 1967, New Zealander Burt Munro set the world record for an Indian motorcycle, on the Bonneville Salt Flats in Utah, of 295.38 km/h. The ane-way course was 8.00 km long. Acceleration rates are often described past the time it takes to accomplish 96.0 km/h from rest. If this fourth dimension was 4.00 s and Burt accelerated at this rate until he reached his maximum speed, how long did it take Burt to complete the course?

[reveal-answer q="fs-id1168057239219″]Show Solution[/reveal-reply]

[hidden-reply a="fs-id1168057239219″]

$96\,\text{km/h}=26.67\,\text{m/s,}\,a=\frac{26.67\,\text{m/s}}{4.0\,\text{s}}=6.67{\text{m/s}}^{2}$

, 295.38 km/h = 82.05 one thousand/s,

$t=12.3\,\text{s}$

fourth dimension to accelerate to maximum speed

$x=504.55\,\text{m}$

distance covered during dispatch

$7495.44\,\text{m}$

at a constant speed

$\frac{7495.44\,\text{m}}{82.05\,\text{m/s}}=91.35\,\text{s}$

so total fourth dimension is

$91.35\,\text{s}+12.3\,\text{s}=103.65\,\text{s}$

[/hidden-answer]

williamsgrely1965.blogspot.com

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/3-6-finding-velocity-and-displacement-from-acceleration/

At What Time Is the Velocity Again Zero? Express Your Answer With the Appropriate Units

3.vi Finding Velocity and Displacement from Acceleration

Learning Objectives

Kinematic Equations from Integral Calculus

Case

Motion of a Motorboat

Strategy

Solution

Significance

Cheque Your Agreement

Summary

Key Equations

Conceptual Questions

Problems

Additional Problems

Claiming Problems

0 Response to "At What Time Is the Velocity Again Zero? Express Your Answer With the Appropriate Units"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel